- que es una compu =P
- MODELO VON NEUMANN
- BUSES::BUSES:: Y MAS BUSES jaja
- NUMEROS 011010100101 0&1#%1& =S
- SISTEMAS BINARIOS JAJA 1+1=0 shaa q viajado..!!
- Sistemas Numericos con Complemento Disminuido a una Base
- numeros numeros y mas numeros =P
- MAPAS??
- CoNTADORES (cuenta cuenta xD)
- AlgEBRA bOOleANA
- LeyES De MORgAn
- MULTIPLEXORES BLA BLA
- Codificadores
- FLIP-FLOP jaja blublu xD
- Inicio
lunes, 8 de diciembre de 2008
MeNu..... ¬¬
Inicio =P
Bueno pues yo no keria y mucho menos tenia pensado hacer un blog ¬¬ blahh q chafa pero ps me siento obligado a hacerlo ya que un profesor nos lo pidio, creo q esto se tomara en cuenta como una calificAcion o algo asi jaja ahh no se ni q pexx conmigo xD
No se que postear pero bueno se supone que lo que debe de contener este "super blog" son todos los temas que vimos en clase asi como tareas y trabajos ¬¬ jaja shaa ya me acorde q no tengo muchos de esos trabajos =S maldita sea ¬¬...
Ps espero terminar este blog o por lo menos meterle aunq sea una entrada a esto jaja sino ps ya ni pexx =P , ahh mi lap esta lenta no se que demonios tiene eso pasa por meterle USB's dañados o virulientos de otros weyes que no formatean sus memorias ¬¬ q fraude
ps ya no se q mas escribir jaja como se dieron cuenta no escribi nada importante jaja y eso no me importa =P yo no keria hacer este blog pero ni pexx yo se q no es obligatorio pero ps necesito esos puntos extras (espero q si este dando puntos extras por lo del blog =S, sino me tendre q ma$%&#ar al wey q me dijo q lo hiciera ¬¬) bueno ps entren a ver q pexx con esto aunq sea para darme animos y saber que alguien esta leyendo esto jaja igual y despues me late escribrir por este medio xD (ojala y no =D)
ps va cuidense pasensela chido y sigan rockeando DuRo..!!
ahh simon se me olvidaba, entren a http://www.sadikorn.tk/ oiganos y pidan sus rolas o mientenos las madres no hay pex jaja
va adiosxx xDD
align=top name="ark">
No se que postear pero bueno se supone que lo que debe de contener este "super blog" son todos los temas que vimos en clase asi como tareas y trabajos ¬¬ jaja shaa ya me acorde q no tengo muchos de esos trabajos =S maldita sea ¬¬...
Ps espero terminar este blog o por lo menos meterle aunq sea una entrada a esto jaja sino ps ya ni pexx =P , ahh mi lap esta lenta no se que demonios tiene eso pasa por meterle USB's dañados o virulientos de otros weyes que no formatean sus memorias ¬¬ q fraude
ps ya no se q mas escribir jaja como se dieron cuenta no escribi nada importante jaja y eso no me importa =P yo no keria hacer este blog pero ni pexx yo se q no es obligatorio pero ps necesito esos puntos extras (espero q si este dando puntos extras por lo del blog =S, sino me tendre q ma$%&#ar al wey q me dijo q lo hiciera ¬¬) bueno ps entren a ver q pexx con esto aunq sea para darme animos y saber que alguien esta leyendo esto jaja igual y despues me late escribrir por este medio xD (ojala y no =D)
ps va cuidense pasensela chido y sigan rockeando DuRo..!!
ahh simon se me olvidaba, entren a http://www.sadikorn.tk/ oiganos y pidan sus rolas o mientenos las madres no hay pex jaja
va adiosxx xDD
Y SI QUIERES SABER QUE ES LA ARKITECTURA DE COMPUTADORAS DALI CLIK A LA IMAGEN xD
align=top name="ark">
Sistemas Numericos con Coplemento Disminuido a una Base
El complemento a uno es un caso particular del complemento disminuido a una base para números binarios y está dado por:
[N] 2 � 1 = 2n - (N)2-1, donde n es el número de bits de (N)2.
Algoritmo para determinar [N]r � 1 dado (N) r.
Reemplazamos cada dígito ai de (N)r por r - 1 - ai. Observe que si r = 2, basta con complementar cada bit individual de (N)r.
Ejemplo.
Sumar: (1001)2 y - (0100)2.
(1001)2: 0 1 0 0 1
- (0100)2: + 1 1 0 1 1
----------------------------
1 0 0 1 0 0
Se obtiene el resultado correcto si el acarreo de salida del bit más significativo se suma a la posición del bit menos significativo. Es decir 00100 + 1 = 00101.
Este procedimiento se conoce como acarreo final circular y es un paso de corrección necesario en la aritmética de complemento disminuido.
Por tanto, + (1001)2 - (0100)2 = (0,0101)2ms = (101)2.
Ejemplo.
Sumar +(1001)2 y - (1111)2
+(1001)2: 0 1 0 0 1
-(1111)2: + 1 0 0 0 0
--------------------------
1 1 0 0 1
El acarreo final circular es 0 y por tanto,
+ (1001)2 - (1111)2 = (1,1001)2ms = - (0,0110)2ms = -(0110)2.
Ejemplo.
Sumar (75)10 y - (21)10
El complemento a nueve de 021 es 978. Por tanto, 075 + 978 = 1053, que es el resultado correcto después del procedimiento de acarreo final circular 053 + 1 = 054.
Ejemplo.
Sumar (21)10 y - (75)10.
El cálculo de 021 + 924 = 945, que es el resultado correcto, pues el acarreo final es cero. Así, (9,45)10ms = - (0,54) 10ms = -(54)10.
CoNTADORES (cuenta cuenta xD)
CONTADORES:
Un contador es un circuito secuencial de aplicación general, cuyas salidas representan en un determinado código el numero de pulsos que se meten a la entrada
Están constituidos por una serie de biestables conectados entre si de modo que las salidas de estos cambian de estado cuando se aplican impulso. a la entrada.
La capacidad de un contador es el numero mas elevado, expresado en cualquiera de los códigos binarios, que puede ser representado en sus salidas.
El modulo, o número de estados totales que puede representar el contador, es igual al numero máximo de impulsos que se puede representar más uno (el cero). Si "n" es el número de flip-flops empleado para hacer el contador, y "M" el módulo del contador, se debe verificar:
M " 2”
Cuando el contador llega al valor máximo de su capacidad, comienza a contar de nuevo desde cero al aplicarle el siguiente impulso.
Dependiendo del modo d e operación, lo s contadores pueden ser ascendentes ( si su contenido se incrementa con cada impulso), descendentes (si su contenido disminuye), o bien una combinación de ambos (up/down counters).
TABLA DE ESTADOS:
Q | Q(t+1) | J | K | D | S | R | T |
0 | 0 | 0 | X | 0 | 0 | X | 0 |
0 | 1 | 1 | X | 1 | 1 | 0 | 1 |
1 | 0 | X | 1 | 0 | 0 | 1 | 1 |
1 | 1 | X | 0 | 1 | X | 0 | 0 |
AlgEBRA bOOleANA
Se denomina función lógica o booleana a aquella función matemática cuyas son binarias y están unidas mediante los operadores del álgebra de Boole suma lógica (+), producto lógico (.) o negación(-).
REPRESENTACIÓN
Existen distintas formas de representar una función lógica, entre las que podemos destacar las siguientes:
REPRESENTACIÓN
Existen distintas formas de representar una función lógica, entre las que podemos destacar las siguientes:
- Algebraica
- Por tabla de verdad
- Numérica
- Gráfica
a) ALGEBRAICA
Ejemplo con distintas formas en las que se puede expresar algebraicamente una misma función de tres variables.
a) F = [(A + BC’)’ + ABC]’ + AB’C
b) F = A’BC’ + AB’C’ + AB’C + ABC’
c) F = (A + B + C)(A + B + C’)(A + B’ + C’)(A’ + B’ + C’)
d) F = BC’ + AB’
e) F = (A + B)(B’ + C’)
f) F = [(BC’)’ · (AB’)’]’
g) F = [(A + B)’ + (B’ + C’)’]’
La expresión a) puede proceder de un problema lógico planteado o del paso de unas especificaciones a lenguaje algebraico. Las formas b) y c) reciben el nombre expresiones canónicas de suma de productos (sum-of-products, SOP, en inglés), la b), y de productos de sumas (product-of-sums, POS, en inglés), la c); su característica principal es la aparición de cada una de las variables (A, B y C) en cada uno de los sumandos o productos. Las d) y e) son funciones simplificadas, esto es, reducidas a su mínima expresión. Las dos últimas expresiones tienen la particularidad de que exclusivamente utiliza funciones NO-Y, la f), o funciones NO-O, la g).
b) TABLA DE VERDAD
Una tabla de verdad contiene todos los valores posibles de una función lógica dependiendo del valor de sus variables. El número de combinaciones posibles para una función de n variables vendrá dado por 2n. Una función lógica puede representarse algebraicamente de distintas formas como acabamos de ver, pero sólo tiene una tabla de verdad.
La forma más cómodo para ver la equivalencia entre una tabla de verdad y una expresión algebraica es cuando esta última se da en su forma canónica. Así, la función canónica de suma de productos
F = A’BC’ + AB’C’ + AB’C + ABC’
nos indica que será 1 cuando lo sea uno de sus sumandos, lo que significa que tendrá por lo tanto cuatro combinaciones que lo serán (010 para A’BC’, 100 para AB’C’, 101 para AB’C y 110 para ABC’) siendo el resto de combiaciones 0. Con la función canónica de producto de sumas se puede razonar de forma análoga, pero en este caso observando que la función será 0 cuando lo sea uno de sus productos. También es fácil obtener la tabla de verdad a partir de la función simplificada, pero no así a la inversa.
c) NUMÉRICA
La representación numérica es una forma simplificada de representar las expresiones canónicas. Si consideramos el criterio de sustituir una variable sin negar por un 1 y una negada por un 0, podremos representar el término, ya sea una suma o un producto, por un número decimal equivalente al valor binario de la combinación. Por ejemplo, los siguientes términos canónicos se representarán del siguiente modo (observe que se toma el orden de A a D como de mayor a menor peso):
AB’CD = 10112 = 1110
A’ + B + C’ + D’ = 01002 = 410
Para representar una función canónica en suma de productos utilizaremos el símbolo Σn (sigma) y en producto de sumas Πn (pi), donde n indicará el número de variables. Así, la representación numérica correspondiente a la tabla de verdad del punto anterior quedará como:
F = Σ3(2, 4, 5, 6) = Π3(0, 1, 3, 7)
Matemáticamente se demuestra, que para todo término i de una función, se cumple la siguiente ecuación:
F = [Σn(i)]' = Πn(2n-1-i )
A modo de ejemplo se puede utilizar esta igualdad para obtener el producto de sumas a partir de la suma de productos del ejemplo anterior:
F = Σ3(2, 4, 5, 6) = [Σ3(2, 4, 5, 6)]' ' = [Σ3(0, 1, 3, 7)]' = Π3(0, 4, 6, 7)
d) GRÁFICA
La representación gráfica es la que se utiliza en circuitos y esquemas electrónicos. En la siguiente figura se representan gráficamente dos funciones algebraicas, una con símbolos no normalizados, superior, y la otra con normalizados, inferior.
Ejemplo con distintas formas en las que se puede expresar algebraicamente una misma función de tres variables.
a) F = [(A + BC’)’ + ABC]’ + AB’C
b) F = A’BC’ + AB’C’ + AB’C + ABC’
c) F = (A + B + C)(A + B + C’)(A + B’ + C’)(A’ + B’ + C’)
d) F = BC’ + AB’
e) F = (A + B)(B’ + C’)
f) F = [(BC’)’ · (AB’)’]’
g) F = [(A + B)’ + (B’ + C’)’]’
La expresión a) puede proceder de un problema lógico planteado o del paso de unas especificaciones a lenguaje algebraico. Las formas b) y c) reciben el nombre expresiones canónicas de suma de productos (sum-of-products, SOP, en inglés), la b), y de productos de sumas (product-of-sums, POS, en inglés), la c); su característica principal es la aparición de cada una de las variables (A, B y C) en cada uno de los sumandos o productos. Las d) y e) son funciones simplificadas, esto es, reducidas a su mínima expresión. Las dos últimas expresiones tienen la particularidad de que exclusivamente utiliza funciones NO-Y, la f), o funciones NO-O, la g).
b) TABLA DE VERDAD
Una tabla de verdad contiene todos los valores posibles de una función lógica dependiendo del valor de sus variables. El número de combinaciones posibles para una función de n variables vendrá dado por 2n. Una función lógica puede representarse algebraicamente de distintas formas como acabamos de ver, pero sólo tiene una tabla de verdad.
La forma más cómodo para ver la equivalencia entre una tabla de verdad y una expresión algebraica es cuando esta última se da en su forma canónica. Así, la función canónica de suma de productos
F = A’BC’ + AB’C’ + AB’C + ABC’
nos indica que será 1 cuando lo sea uno de sus sumandos, lo que significa que tendrá por lo tanto cuatro combinaciones que lo serán (010 para A’BC’, 100 para AB’C’, 101 para AB’C y 110 para ABC’) siendo el resto de combiaciones 0. Con la función canónica de producto de sumas se puede razonar de forma análoga, pero en este caso observando que la función será 0 cuando lo sea uno de sus productos. También es fácil obtener la tabla de verdad a partir de la función simplificada, pero no así a la inversa.
c) NUMÉRICA
La representación numérica es una forma simplificada de representar las expresiones canónicas. Si consideramos el criterio de sustituir una variable sin negar por un 1 y una negada por un 0, podremos representar el término, ya sea una suma o un producto, por un número decimal equivalente al valor binario de la combinación. Por ejemplo, los siguientes términos canónicos se representarán del siguiente modo (observe que se toma el orden de A a D como de mayor a menor peso):
AB’CD = 10112 = 1110
A’ + B + C’ + D’ = 01002 = 410
Para representar una función canónica en suma de productos utilizaremos el símbolo Σn (sigma) y en producto de sumas Πn (pi), donde n indicará el número de variables. Así, la representación numérica correspondiente a la tabla de verdad del punto anterior quedará como:
F = Σ3(2, 4, 5, 6) = Π3(0, 1, 3, 7)
Matemáticamente se demuestra, que para todo término i de una función, se cumple la siguiente ecuación:
F = [Σn(i)]' = Πn(2n-1-i )
A modo de ejemplo se puede utilizar esta igualdad para obtener el producto de sumas a partir de la suma de productos del ejemplo anterior:
F = Σ3(2, 4, 5, 6) = [Σ3(2, 4, 5, 6)]' ' = [Σ3(0, 1, 3, 7)]' = Π3(0, 4, 6, 7)
d) GRÁFICA
La representación gráfica es la que se utiliza en circuitos y esquemas electrónicos. En la siguiente figura se representan gráficamente dos funciones algebraicas, una con símbolos no normalizados, superior, y la otra con normalizados, inferior.
LeyES De MORgAn
Las leyes de De Morgan declaran que la suma de n variables globalmente negadas (o invertidas) es igual al producto de las n variables negadas individualmente; y que inversamente, el producto de n variables globalmente negadas es igual a la suma de las n variables negadas individualmente.
Prueba.
 | |||||||||
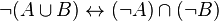| A | B |  |  |  |  |  | |||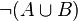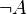
| V | V | V | F | F | F | F | |||
| V | F | V | F | F | V | F | |||
| F | V | V | F | V | F | F | |||
| F | F | F | V | V | V | V | |||
Con n Proposiciones
La prueba utiliza la asociatividad y la distributividad de las leyes 
y 
.
- Verdad
- Si verdad por n
COMPUERTAS LOGICAS....
Las compuertas son bloques del hardware que producen señales en binario 1 ó 0 cuando se satisfacen los requisitos de entrada lógica. Las diversas compuertas lógicas se encuentran comúnmente en sistemas de computadoras digitales. Cada compuerta tiene un símbolo gráfico diferente y su operación puede describirse por medio de una función algebraica. Las relaciones entrada - salida de las variables binarias para cada compuerta pueden representarse en forma tabular en una tabla de verdad.
A continuación se detallan los nombres, símbolos, gráficos, funciones algebraicas, y tablas de verdad de las compuertas más usadas.
Cada compuerta tiene dos variables de entrada designadas por A y B y una salida binaria designada por x. |
|
La compuerta OR produce la función sumadora, esto es, la salida es 1 si la entrada A o la entrada B o ambas entradas son 1; de otra manera, la salida es 0. |
|
El circuito NOT es un inversor que invierte el nivel lógico de una señal binaria. Produce el NOT, o función complementaria. El símbolo algebraico utilizado para el complemento es una barra sobra el símbolo de la variable binaria. |
|
Compuerta Separador (yes): Un símbolo triángulo por sí mismo designa un circuito separador, el cual no produce ninguna función lógica particular puesto que el valor binario de la salida es el mismo de la entrada. |
|
Es el complemento de la función AND, como se indica por el símbolo gráfico, que consiste en una compuerta AND seguida por un pequeño círculo (quiere decir que invierte la señal). |
|
La compuerta NOR es el complemento de la compuerta OR y utiliza el símbolo de la compuerta OR seguido de un círculo pequeño (quiere decir que invierte la señal). Las compuertas NOR pueden tener más de dos entradas, y la salida es siempre el complemento de la función OR. |
|
domingo, 7 de diciembre de 2008
FLIP-FLOP jaja blublu xD
Dispositivo de almacenamiento temporal de dos estados (alto y bajo). El biestable T cambia de estado ("toggle" en inglés) cada vez que la entrada de sincronismo o de reloj se dispara. Si la entrada T está a nivel bajo, el biestable retiene el nivel previo. Puede obtenerse al unir las entradas de control de un biestable JK, unión que se corresponde a la entrada T.
Descripción
Cronograma del biestable RS
Dispositivo de almacenamiento temporal de dos estados (alto y bajo), cuyas entradas principales, R y S, a las que debe el nombre, permiten al ser activadas:
R: el borrado (reset en inglés), puesta a 0 ó nivel bajo de la salida.
S: el grabado (set en inglés), puesta a 1 ó nivel alto de la salida.
Si no se activa ninguna de las entradas, el biestable permanece en el estado que poseía tras la última operación de borrado o grabado. En ningún caso deberían activarse ambas entradas a la vez, ya que esto provoca que las salidas directa (Q) y negada (Q') queden con el mismo valor: a bajo, si la báscula está construida con puertas NO-O (NOR), o a alto, si con puertas NO-Y (NAND). El problema de que ambas salidas queden al mismo estado está en que al desactivar ambas entradas no se podrá determinar el estado en el que quedaría la salida. Por eso, en las tablas de verdad, la activación de ambas entradas se contempla como caso no deseado (N. D.).
Descripción
Cronograma del biestable RS
Dispositivo de almacenamiento temporal de dos estados (alto y bajo), cuyas entradas principales, R y S, a las que debe el nombre, permiten al ser activadas:
R: el borrado (reset en inglés), puesta a 0 ó nivel bajo de la salida.
S: el grabado (set en inglés), puesta a 1 ó nivel alto de la salida.
Si no se activa ninguna de las entradas, el biestable permanece en el estado que poseía tras la última operación de borrado o grabado. En ningún caso deberían activarse ambas entradas a la vez, ya que esto provoca que las salidas directa (Q) y negada (Q') queden con el mismo valor: a bajo, si la báscula está construida con puertas NO-O (NOR), o a alto, si con puertas NO-Y (NAND). El problema de que ambas salidas queden al mismo estado está en que al desactivar ambas entradas no se podrá determinar el estado en el que quedaría la salida. Por eso, en las tablas de verdad, la activación de ambas entradas se contempla como caso no deseado (N. D.).
Su tabla de verdad es la siguiente (Q representa el estado actual de la salida y q el estado anterior a la última activación):
Tabla de verdad biestable RS
Codificadores
LOS CODIFICADORES
Al diseñar un sistema digital es necesario representar o codificar en forma binaria la información numérica y alfanumérica que se obtiene de dicho sistema y, para ello, existen los circuitos combinatorios denominados codificadores.
Un codificador es un circuito combinatorio que cuenta con un número determinado de entradas, de las cuales sólo una tiene el estado lógico 1, y se genera un código de varios bits que depende de cuál sea la entrada excitada.
Diagrama de bloques de un codificador de 10 entradas y 4 salidas
Para ilustrar esto mejor pongamos un ejemplo. Supongamos que queremos transmitir un código binario con cada una de las pulsaciones de un teclado númerico, como puede ser el de una calculadora, en éste existen diez dígitos y al menos seis caracteres especiales y, si consideramos sólo las diez cifras, esta condición la podemos satisfacer con cuatro bit. Pero variemos el circuito de la calculadora para entender mejor el ejemplo. Modifiquemos el teclado de tal manera que al presionar una tecla se cierre el pulsador que conectará una línea de entrada.
En el interior del bloque podemos imaginar unos conductores cruzados que unen entradas y salidas entre sí. Veamos cómo han de conectarse a fin de que den los códigos deseados. Para representar los códigos de salida utilizaremos el denominado código BCD. La tabla de verdad que define este codificador es la siguiente:
Cuando alguna de las entradas está a 1, quiere decir que el pulsador correspondiente está accionado. Como suponemos que no hay más que un pulsador activado simultáneamente, entonces en cualquier línea de la tabla todas las entradas excepto una serán 0.
A partir de la tabla se deduce que la salida Y1 será 1 si lo es la entrada 9, ó la 7, ó la 5, ó la 3, ó la 1, de ahí que la ecuación booleana correspondiente a esta salida sea la suma de las entradas 1, 3, 5, 7 y 9. Si seguimos analizando la tabla obtendremos, de forma análoga, las ecuaciones que tienen que cumplir las salidas Y2, Y3 e Y4.
Cada una de las ecuaciones que salen de la tabla de verdad se podrán componer con puertas OR, construidas con diodos. En nuestro ejemplo, el bloque que antes habíamos diseñado imaginariamente con una trama de conductores, ahora lo conectaremos a través de diodos; y a este nuevo bloque lo denominaremos matriz de diodos.
Los tipos de codificadores más usuales en el mercado son los de matrices de diodos
Todos los diodos del codificador pueden ser sustituidos por otro correspondiente formado por la base y el emisor de un transistor. Si el colector se une a la tensión de alimentación, entonces resulta una puerta OR seguidor de emisor.
Por otro lado, en realidad sólo se requiere un transistor con emisor múltiple para cada entrada del codificador. La base está unida a la línea de entrada, y cada emisor se conecta a una línea de salida diferente de acuerdo con la lógica del codificador. Por ejemplo, la línea de entrada 7 está unida a tres diodos cuyos cátodos van a las salidas 1, 2 y 3; esta combinación puede ser sustituida por un transistor de tres emisores, conectado como se indica en la figura. El número máximo de emisores que se puede necesitar es igual al número de bits del código de salida.
Normalmente un codificador utiliza niveles de salida TTL. Si cada línea de salida del codificador va a la entrada de datos de una formación tótem, tendremos una salida en tótem. Si, por el contrario, conectamos dicha salida a la entrada de datos de una etapa de colector abierto, estaremos ante una salida en colector abierto.
Dentro de los codificadores podemos distinguir varios tipos, como el descrito anteriormente de células con diodos, y los denominados codificadores con prioridad.
Codificadores con prioridad y señal de habilitación
Circuito integrado típico de un codificador con prioridad
Vamos a prescindir ahora de la condición supuesta anteriormente y referida a que en cualquier momento sólo puede haber un pulsador accionado. Si, de un modo fortuito, se pulsan simultáneamente varias teclas, vamos a dar prioridad y codificar la línea de datos de orden superior. Por ejemplo, si se excitan las entradas 5 y 6, lo que se desea es que la salida sea la que corresponde a la entrada 6. Para seguir el mismo procedimiento, a fin de entender este tipo de codificadores, describamos su tabla de verdad:
Esta tabla corresponde a un codificador con prioridad de 10 a 4 líneas. La X indica que esa entrada puede tomar cualquier valor, es decir, puede ser 0 ó 1, por lo que el estado X es irrelevante. No obstante, ahora habrá que tener en cuenta un 0 en la tabla, mientras que en el caso anterior podíamos ignorarlo, ya que dicha tabla viene determinada únicamente por los 1 en su diagonal. Si analizáramos los distintos valores que toman las salidas, e intentáramos expresar su ecuación booleana correspondiente, veríamos que son ecuaciones bastantes complicadas.
Para construir mediante puertas la tabla de verdad anteriormente citada, se utilizarán puertas AND-OR de dos y cuatro entradas. Normalmente, este tipo de lógica se fabrica en un chip integrado a escala media, cuya prioridad codifica diez líneas - decimal a cuatro líneas BCD.
Entre las aplicaciones de este tipo de codificadores destacan la codificación de pequeños teclados, la conversión analógica a digital y el control de perturbaciones en los ordenadores.
Finalmente, señalaremos que la mayor aplicación de los codificadores se da en el campo de la construcción, a partir de ellos mismos, de los denominados multiplexores.
MULTIPLEXORES BLA BLA
LOS MULTIPLEXORES
Mediante una señal de control deseamos seleccionar una de las entradas y que ésta aparezca a la salida. Haciendo una analogía eléctrica, podemos comparar un multiplexor con un conmutador de varias posiciones, de manera que, situando el selector en una de las posibles entradas, ésta aparecerá en la salida.
Los multiplexores son ircuitos combinacionales con varias entradas y una salida de datos, y están dotados de entradas de control capaces de seleccionar una, y sólo una, de las entradas de datos para permitir su transmisión desde la entrada seleccionada a la salida que es única.La entrada seleccionada viene determinada por la combinación de ceros (0) y unos (1) lógicos en las entradas de control. La cantidad que necesitaremos será igual a la potencia de 2 que resulte de analizar el número de entradas. Así, por ejemplo, a un multiplexor de 8 entradas le corresponderán 3 de control.
Podemos decir que la función de un multiplexor consiste en seleccionar una de entre un número de líneas de entrada y transmitir el dato de un canal de información único. Por lo tanto, es equivalente a un conmutador de varias entradas y una salida.
Dentro de un multiplexor hay que destacar tres tipos de señales: los datos de entrada, las entradas de control y la salida
El diseño de un multiplexor se realiza de la misma manera que cualquier sistema combinatorio desarrollado hasta ahora. Veamos, como ejemplo, el caso de un multiplexor de cuatro entradas y una salida que tendrá, según lo dicho anteriormente, dos entradas de control. Esta tabla de verdad define claramente cómo, dependiendo de la combinación de las entradas de control, a la salida se transmite una u otra entrada de las cuatro posibles. Así:
S = (/A*/B*I0) + (/A*B*I1) + (A*/B*I2) + (A*B*I3)
La estructura de los multiplexores es siempre muy parecida a esta que hemos descrito, aunque a veces se añade otra entrada suplementaria de validación o habilitación, denominada «strobe» o «enable» que, aplicada a las puertas AND, produce la presentación de la salida.
Tipos de multiplexores
Dentro de la gran variedad de multiplexores que existen en el mercado, hay varios tipos que conviene destacar a causa de su gran utilidad en circuitos digitales, éstos son:
Multiplexor de 8 entradas.
Multiplexor de 16 entradas.
Doble multiplexor de 4 entradas.
Dentro del primer tipo podemos hacer la distinción entre tener la entrada de «strobe» o no. La tecnología utilizada para su diseño es TTL, de alta integración, y la potencia que disipan suele ser de unos 150 mW. El tiempo de retardo típico es de unos 25 nanosegundos y tienen un "fan - out" de 10. Normalmente, estos circuitos suelen darnos dos tipos de salida: una afirmada y la otra negada.
En cuanto al segundo tipo de multiplexores, señalaremos que se diferencian de los primeros en el número de entradas, que es el doble, y que no existe la posibilidad de tener dos salidas, sino que sólo podemos optar por la negada y, en consecuencia, a la salida únicamente se tendrán los datos de la entrada complementados. La potencia de disipación para estos multiplexores viene a ser de aproximadamente unos 200 mW. El tiempo de retardo y el "fan - out" son más o menos iguales que en el caso del multiplexor de 8 entradas.
Diagrama básico de un multiplexor de 16 entradas y 2 señales de control
En la ilustración correspondiente podemos ver un multiplexor de 16 entradas, donde, si hacemos 0 el «strobe», en la salida se obtiene el dato negado de la entrada seleccionada mediante las cuatro entradas de control.
En el último de los tipos, dentro del mismo encapsulado del circuito integrado, tenemos dos multiplexores de cuatro entradas de datos: dos de control y una señal de «strobe» cada uno.
Doble multiplexor de cuatro entradas donde las señales de control son comunes
Las entradas de control son comunes para ambos multiplexores, como podemos ver en el circuito de la figura. Al igual que los anteriores, se suelen realizar con tecnología TTL de alta integración, y tienen una disipación media de unos 180 mW.
Con estos tres tipos de multiplexores trabajaremos habitualmente, incluso en el caso de tener que emplear algún otro de orden superior, es decir, con mayor número de entradas. Para ello, necesitaremos utilizar más de un multiplexor de los descritos anteriormente.
Multiplexor de 32 entradas construido a partir de cuatro multiplexores de 8 entradas y uno de 4 entradas.
La forma de conectarlos entre sí depende de la aplicación concreta de que se trate, pero siempre habrá que disponer de más de una etapa de multiplexores, lo cual acarrea un tiempo de retardo. Así, por ejemplo, para seleccionar un dato de entre las 32 entradas de que disponemos, deberemos diseñar un sistema análogo al representado en la figura correspondiente.
El primer multiplexor de 8 entradas sitúa secuencialmente los datos de entrada I0 a I7 en la línea de salida de éste, a medida que el código de las señales de control va variando. Análogamente, el segundo multiplexor, también de 8 entradas, transmitirá los datos I8 a I15 a su línea de salida, dependiendo de las señales de control.
Diagrama de conexión de un circuito integrado que contiene un multiplexor de 8 entradas y señal de <
Estas entradas de control están unidas entre sí de manera que cuando, por ejemplo, aparece en la línea de salida del primer multiplexor I1, en la salida del segundo estará I9, en la del tercero I17 y en la del último I25. Si queremos sacar a la salida del conjunto de multiplexores cualquiera de las líneas de salida anteriormente citadas, necesitaremos utilizar un multiplexor de 4 entradas y, con sus señales de control, activaremos la entrada que nosotros deseemos. Así, por ejemplo, para tener en la salida final la línea de entrada I1, habría que poner en el último multiplexor de 4 entradas la combinación 00 en sus señales de control.
Por último, destacaremos que los multiplexores, además de seleccionar datos, tienen otras aplicaciones importantes, a saber:
- La conversión paralelo - serie. Como puede ser conducir la salida en paralelo de un ordenador hacia un terminal remoto a través de una línea de transmisión serie.
- La generación de funciones para lógica combinatoria.
MAPAS??
Mapas de Karnaugh
Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables.
Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a "1". Si A en la tabla de verdad es "0" se pone A, si B = "1" se pone B, Si C = "0" se pone C, etc.
Ejemplo: Se tiene la siguiente tabla de verdad para tres variables.
Se desarrolla la función lógica basada en ella. (primera forma canónica). Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a "1". Si A en la tabla de verdad es "0" se pone A, si B = "1" se pone B, Si C = "0" se pone C, etc.
F = A B C + A B C + A B C + A B C + A B C + A B C
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh.
Este mapa tiene 8 casillas que corresponden a 2n, donde n = 3 (número de variables (A, B, C))
La primera fila corresponde a A = 0
La segunda fila corresponde a A = 1
La primera columna corresponde a BC = 00 (B=0 y C=0)
La segunda columna corresponde a BC = 01 (B=0 y C=1)
La tercera columna corresponde a BC = 11 (B=1 y C=1)
La cuarta columna corresponde a BC = 10 (B=1 y C=0)
En el mapa de Karnaugh se han puesto "1" en las casillas que corresponden a los valores de F = "1" en la tabla de verdad.
Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.
Para proceder con la simplificación, se crean grupos de "1"s que tengan 1, 2, 4, 8, 16, etc. (sólo potencias de 2).
Los "1"s deben estar adyacentes (no en diagonal) y mientras más "1"s tenga el grupo, mejor.
La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de "1"s en cada grupo
La nueva expresión de la función boolena simplificada se deduce del mapa de Karnaugh.
- Para el primer grupo (rojo): la simplificación da B (los "1"s de la tercera y cuarta columna) corresponden a B sin negar)- Para el segundo grupo (azul): la simplificación da A (los "1"s están en la fila inferior que corresponde a A sin negar)
Entonces el resultado es F = B + A ó F = A + B
Ejemplo:
Una tabla de verdad como la de la, izquierda da la siguiente función booleana:
F = A B C + A B C + A B C + A B C
Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = "1"
Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos. Se lograron hacer 3 grupos de dos "1"s cada uno.
Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.
La función simplificada es:
F = A B + A C + B C
Grupo en azul: AB, grupo marrón:AC, grupo verde:BC
Suscribirse a:
Entradas (Atom)